- 股票掌故
- 香港股票資訊
- 神州股票資訊
- 台股資訊
- 博客好文
- 文庫舊文
- 香港股票資訊
- 第一財經
- 微信公眾號
- Webb哥點將錄
- 港股專區
- 股海挪亞方舟
- 動漫遊戲音樂
- 好歌
- 動漫綜合
- RealBlog
- 測試
- 強國
- 潮流潮物 [Fashion board]
- 龍鳳大茶樓
- 文章保管庫
- 財經人物
- 智慧
- 世界之大,無奇不有
- 創業
- 股壇維基研發區
- 英文
- 財經書籍
- 期權期指輪天地
- 郊遊遠足
- 站務
- 飲食
- 國際經濟
- 上市公司新聞
- 美股專區
- 書藉及文章分享區
- 娛樂廣場
- 波馬風雲
- 政治民生區
- 財經專業機構
- 識飲色食
- 即市討論區
- 股票專業討論區
- 全球政治經濟社會區
- 建築
- I.T.
- 馬後砲膠區之圖表
- 打工仔
- 蘋果專欄
- 雨傘革命
- Louis 先生投資時事分享區
- 地產
Random Tags
金融詞彙(10):債券定價原理 (Bond-Pricing Theorem)+投資策略 寗零
http://notcomment.com/wp/3895債券定價原理
定理一:債券的市場價格與到期收益率(ytm)呈反比關係。 即到期收益率上升時,債券價格會下跌。 反之,到期收益率下降時,債券價格會上升。
定理二:當債券的收益率不變,即債券的息票率與收益率之間的差額固定不變時,債券的到期時間與債券價格的波動幅度之間成正比關係。 即到期時間越長,價格波動幅度越大;反之,到期時間越短,價格波動幅度越小。
定理三:隨著債券到期時間的臨近,債券價格的波動幅度減少,並且是以遞增的速度減少; 反之,到期時間越長,債券價格波動幅度增加,並且是以遞減的速度增加。
定理四:對於期限既定的債券,由收益率下降導致的債券價格上升的幅度,大於同等幅度的收益率上升,導致的債券價格下降的幅度。即對於同等幅度的收益率變動,收益率下降給投資者帶來的利潤,大於收益率上升給投資者帶來的損失。
定理五:對於給定的收益率變動幅度,債券的息票率與債券價格的波動幅度之間成反比關係。即息票率越高,債券價格的波動幅度越小。
投資債券的有關風險:
利率風險(亦稱市場風險)interest rate risk
再投資風險reinvestment risk
回購風險call risk
信用(違約)風險default risk
收益率曲線(存續期)風險duration risk
通脹(購買力)風險inflation risk
外匯風險foreign exchange risk
簡單投資債券策略:
1.如預期市場利率下跌,買入票息低及到期期限長的債券。
2.如預期市場利率上升,買入票息高及到期期限短的債券。
3.買入持有法,持有債券直至到期日,取回面值,不受債券價格升跌影響。
所以你現在知道,為什麼筆者前幾天建議大家,可以考慮買入一些你喜歡的中國地產美元債券,不過不要超過2017年啊!最好就是到2015年然後轉回返港紙,希望有機會完我的港紙夢(請看筆者2013年9月寫的文章)!
還有,筆者一般都是buy and hold,做我的banker就無mud錢賺呢!
債市那麼大,要慢慢選擇啊!
以下筆者拍於貴州省貴陽息烽的市場上,當地人大多用這環保籃。你們選擇債券也要像她慢慢來,不然就買了蘿低橙就糟糕啦!
金融詞彙(10):債券定價原理 (Bond-Pricing Theorem)+投資策略 寗零
http://notcomment.com/wp/?p=3895債券定價原理
定理一:債券的市場價格與到期收益率(ytm)呈反比關係。 即到期收益率上升時,債券價格會下跌。 反之,到期收益率下降時,債券價格會上升。
定理二:當債券的收益率不變,即債券的息票率與收益率之間的差額固定不變時,債券的到期時間與債券價格的波動幅度之間成正比關係。 即到期時間越長,價格波動幅度越大;反之,到期時間越短,價格波動幅度越小。
定理三:隨著債券到期時間的臨近,債券價格的波動幅度減少,並且是以遞增的速度減少; 反之,到期時間越長,債券價格波動幅度增加,並且是以遞減的速度增加。
定理四:對於期限既定的債券,由收益率下降導致的債券價格上升的幅度,大於同等幅度的收益率上升,導致的債券價格下降的幅度。即對於同等幅度的收益率變動,收益率下降給投資者帶來的利潤,大於收益率上升給投資者帶來的損失。
定理五:對於給定的收益率變動幅度,債券的息票率與債券價格的波動幅度之間成反比關係。即息票率越高,債券價格的波動幅度越小。
投資債券的有關風險:
利率風險(亦稱市場風險)interest rate risk
再投資風險reinvestment risk
回購風險call risk
信用(違約)風險default risk
收益率曲線(存續期)風險duration risk
通脹(購買力)風險inflation risk
外匯風險foreign exchange risk
簡單投資債券策略:
1.如預期市場利率下跌,買入票息低及到期期限長的債券。
2.如預期市場利率上升,買入票息高及到期期限短的債券。
3.買入持有法,持有債券直至到期日,取回面值,不受債券價格升跌影響。
所以你現在知道,為什麼筆者前幾天建議大家,可以考慮買入一些你喜歡的中國地產美元債券,不過不要超過2017年啊!最好就是到2015年然後轉回返港紙,希望有機會完我的港紙夢(請看筆者2013年9月寫的文章)!
還有,筆者一般都是buy and hold,做我的banker就無mud錢賺呢!
債市那麼大,要慢慢選擇啊!
以下筆者拍於貴州省貴陽息烽的市場上,當地人大多用這環保籃。你們選擇債券也要像她慢慢來,不然就買了蘿低橙就糟糕啦!
讀書札記170116不當行為(九)「寇斯(不)定理Coase (In)theorem」
來源: http://www.tangsbookclub.com/2017/01/16/%e8%ae%80%e6%9b%b8%e6%9c%ad%e8%a8%98170116%e4%b8%8d%e7%95%b6%e8%a1%8c%e7%82%ba%ef%bc%88%e4%b9%9d%ef%bc%89%e3%80%8c%e5%af%87%e6%96%af%ef%bc%88%e4%b8%8d%ef%bc%89%e5%ae%9a%e7%90%86coase-intheorem/讀書札記170116
不當行為(九)「寇斯(不)定理Coase (In)theorem」
朝日執筆
上集講到,「稟賦效應」的發現,對經典的「寇斯定理Coase Theorem」造成衝擊。照以往的做法,朝日當然要先解釋一下什麼是「寇斯定理」。
「寇斯定理」的成立有兩個前提。其一是「交易成本」趨近零,*** 即各當事方之間的交易是暢順無礙的。 其二是涉及的利害關係,相對於各當事方的總財富而言,並非是「重大」的。如果是「靠嗰廿皮開飯」的情況,「寇斯定理」就未必適用。不過一般基礎教科書說「寇斯定理」時,都只會強調第一個「前提」,而較少會提到第二個「前提」。
在上述兩個前提下,「寇斯定理」的最簡單表述為:「無論最初的擁有權誰屬,資源總會流向能發揮其最高價值之處。」*****
經典的例子就是「羊麥爭地」。
情境9a1:有一個種小麥的農夫與他養羊的鄰居,對二人地界邊緣的幾塊土地的所有權向來有爭拗。農夫在其中一塊「爭議地」種了一些「優質小麥」,但牧羊人卻把羊群趕到那裏去放牧,於是羊就把一部分的「優質小麥」吃掉了。農夫計算過,如果情況持續,那塊田的「優質小麥」都會被羊吃光,年底他的利潤折合將會損失$150,000。因此他遂把鄰居告上法庭,讓青天大老爺判定地權誰屬。另一方面,牧羊人也算過,如果每天都讓羊去吃「優質小麥」,羊群會生長得更好,這樣會令他可望在年底增加$100,000的利潤。
根據「寇斯定理」,大老爺的判決,其實並不會影響那塊地(及其上的小麥)最終的用途。因為如果他判「9a1地段」的地權屬於農夫,農夫當然會繼續種他的「優質小麥」,並借用公權力(例如報警)把牧羊人和他的羊趕走(假設他們都奉公守法)。相反,如果法官判地權屬於牧羊人,由於農夫在該地種小麥的利潤較高,他必然會願意用(高於$100,000而低於$150,000的)錢,對牧羊人作出補償,以換取他不把羊群趕到「9a1地段」放牧。總之,無論如何那塊地最終都會被用來做價值最高的作業—「種小麥」!
情境9a2:在另一塊「爭議地」,由於土質較差,所以農夫只種了一些「廉價小麥」,牧羊人也同樣把羊群趕到那裏去吃他的「廉價小麥」。農夫計算過,如果情況持續,那塊田的「廉價小麥」都會被羊吃光,年底他的利潤折合將會損失$50,000。因此他又把鄰居告上法庭,讓青天大老爺判定地權誰屬了。另一方面,對羊來說「廉價小麥」和「優質小麥」沒有多大的差別。因此,如果牧羊人每天都讓羊去吃「廉價小麥」,年底的利潤同樣可望增加$100,000。
同樣道理,法官對「9a2地段」的地權判決,也不會影響那塊地最終的用途。因為如果他判地權屬於牧羊人,牧羊人當然會繼續放牧。然而,即使法官判「9a2地段」的地權屬於農夫,由於牧羊人放羊去吃小麥的利潤較高,他也必然會與農夫協商,由牧羊人給農夫作出(低於$100,000而高於$50,000的)補償,以換取農夫容許他繼續在「9a2地段」放牧。總之,無論如何那塊地最終都會被用來做價值最高的作業—「牧羊」!
實在太精妙了!(朝日猶記得當年,初拜讀大師如此精深的劍法時,著實興奮了好一陣!)
「寇斯定理」的理念,被廣泛應用於不同的學門,其中又以「公共政策」和「法學」最為「㗳糖」。對於「法學」中的「經濟分析學派」,「寇斯定理」甚至被奉為不成文的「核心教條」。按該派宗師,由1981年起即擔任 聯邦第七巡迴法院法官至今的 波斯納法官Richard Posner的說法,法官的大部分工作就是判定「權利(產權)誰屬」,這往往是極其困難且易於出錯的。不過,根據「寇斯定理」,錯誤的判決儘管令個別當事人蒙受不幸,但只要法庭對某特定權利的歸屬,作出「肯定的判決」,社會的整體效益並不會被減少,因為資源總會流向能發揮最大效用的地方。***** 換句話說,法官無論判對判錯,反正怎樣判也不會「阻住個地球(的資源)轉」,最多只是決定了資源開始的位置,和「轉的方向」而已。
儘管寇斯在提出「寇斯定理」的那篇論文中就已經明示,其本人並不認為此理論是對現實世界的有效描述—因為寇斯認為「交易成本趨近零」的假設顯然不切實際(雖然後來「寇斯定理」的引用者,好像都忘了這一點。)。然而,「馬克杯市場」實驗卻顯示,即使是在交易成本「趨近零」的情況下,市場的運作也未必如寇斯所料。
在最初用作「熱身圈」的幾個「代幣交易」回合中,受測學生的確如「寇斯定理」所預期,「代幣估值」較高的學生,如果本身已獲派「代幣」,會傾向持有,如果本來未獲分派「代幣」,也會從「代值估值」較低的學生手中,把「代幣」買回來。於是,代表著「資源」的「代幣」,最終果然流向對它們「估值」最高的人手中,也可說是「代幣」都能發揮「最大的價值」。


如果「寇斯定理」是正確的話,即使把交易的貨物,由「可換成具體金額的代幣」,變成「馬克杯」,應該也能作出同樣準確的預測。畢竟,儘管每隻馬克杯都是一模一樣,但每個人對馬克杯的喜愛程度卻不可能完全相同。用經濟學的說法,馬克杯對每個人產生的「效用」有差異。因此他們對「同質Homogeneous」的馬克杯會有不同的「估值」,並能按此相異的「估值」,由高至低排出「估值序列」,正如之前的「代幣市場」一樣。(圖表17A)
可是,當二十二隻馬克杯,如同「代幣實驗」時一般,隨機分配予其中二十二名學生時,全體學生的交易行為,卻與「代幣市場」有明顯差異。(圖表17B)
按照「寇斯定理」,他們應該像在之前的「代幣實驗」一樣,平均作出11宗交易。因為這個數量的「平均交易宗數」,才足以讓作為「資源」的馬克杯,流到對馬克杯「估值最高」的二十二人手中。(圖表17C)

然而,由於「稟賦效應」的存在,潛在買方的平均出價,只及潛在賣方平均叫價的一半,實際上的成交宗數遠遜預期。(圖表17D)
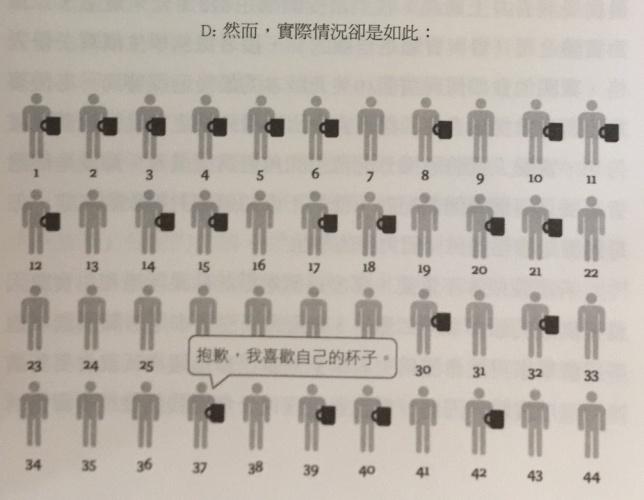
換句話說,「寇斯定理」在理論上,或者在柏拉圖的「理念世界」中,確實是正確無誤的。代幣交易後兌換現金的實驗,結果與「寇斯定理」的預期高度吻合,證實了這一點。不過,當在較貼近實際生活,也就是交易品被換成「額頭無鑿住值(可以換到)幾多錢」的真實商品(例如馬克杯)時,就不那麼靈光了。
「寇斯定理」就是一條非常典型,由經濟學的「公理」—「理性人假設」,「演繹」出來的一條定律。這條定律的「邏輯推導」過程是非常嚴謹的,作為一條「規範性理論」,只要前提正確,以這種方式推導出來的「定律」,一定是「無死法」的!
相反,用以質疑「寇斯定理」是否能有效準確描述現實的「稟賦效應理論」,則是典型由「實驗結果」,「歸納」出來的「描述性理論」。這樣產生的「理論」,無疑只能是「暫準的」,但也通常是「有效的」。
最後,與大家分享一個作者Thaler自己,有關「寇斯理論」應用的反面教材故事。(故事細節經朝日改寫,自不待言。)
情境9b:Thaler花園中靠近一位「友好鄰居」的一邊,種了一棵漂亮的木棉樹。每逢春天「紅棉盛放,天氣暖洋洋」,Thaler很喜歡欣賞木棉花的美態。換句話說,木棉樹的存在為Thaler帶來「正效用」。然而,由於風向關係,到了夏天「結棉籽,借風飄」之時,所有的棉絮都會飄落在鄰居深深的庭院當中,令鄰居疲於清掃。木棉樹的存在,為鄰居帶來的是「負效用」。
鄰居為此感到相當苦惱,他也認同木棉樹及其所在地的產權屬Thaler所有,所以好言與Thaler協商,希望他可以把樹移走。Thaler不希望損失木棉帶來的「正效用」。 他找「樹木專家」作評估,如果把樹移到花園的另一邊,費用大約是US$1,000。(還沒有發達的)Thaler當然付不起。
不過作為經濟學家,Thaler熟諳「寇斯定理」。於是他拍門向鄰居建議,如果對方願意出錢的話,他本人並不介意把樹移到花園的另一邊。只可惜,Thaler連價錢也還沒來得及開,「黑面」的鄰居已經把門狠狠地帶上。接下來的一個月,向來友善的他對Thaler都是一副「鞋口鞋面」,連招呼也沒有打一聲……
關於方法學的問題,暫時到此為止。下一集將會為各位繼續介紹其他「行為經濟學」的理論和研究課題。
P.S. 文中提到的波斯納法官,可謂著作等身。朝日在此推薦他與「理性派」經濟學大師貝加Gary Becker合著的一本「入門級」散文集──《胖子的脂肪該被抽稅嗎?》(為二人的網誌文章合集)。內容輕鬆有趣之餘,SENSE量卻頗為充盈。
09集關鍵字:
寇斯定理Coase Theorem
羊麥爭地
資源總會流向能發揮其最高價值之處
法律經濟分析學派
代幣/馬克杯交易市場
《不當行為》Richard Thaler著/劉怡女 譯
Next Page