- 股票掌故
- 香港股票資訊
- 神州股票資訊
- 台股資訊
- 博客好文
- 文庫舊文
- 香港股票資訊
- 第一財經
- 微信公眾號
- Webb哥點將錄
- 港股專區
- 股海挪亞方舟
- 動漫遊戲音樂
- 好歌
- 動漫綜合
- RealBlog
- 測試
- 強國
- 潮流潮物 [Fashion board]
- 龍鳳大茶樓
- 文章保管庫
- 財經人物
- 智慧
- 世界之大,無奇不有
- 創業
- 股壇維基研發區
- 英文
- 財經書籍
- 期權期指輪天地
- 郊遊遠足
- 站務
- 飲食
- 國際經濟
- 上市公司新聞
- 美股專區
- 書藉及文章分享區
- 娛樂廣場
- 波馬風雲
- 政治民生區
- 財經專業機構
- 識飲色食
- 即市討論區
- 股票專業討論區
- 全球政治經濟社會區
- 建築
- I.T.
- 馬後砲膠區之圖表
- 打工仔
- 蘋果專欄
- 雨傘革命
- Louis 先生投資時事分享區
- 地產
Random Tags
30年期美債定價疑雲:債券交易員數學不好?
來源: http://wallstreetcn.com/node/209839隔夜美國30年期國債期貨(2015年6月到期)價格出現了十分詭異的波動。在收盤前兩小時價格僅有145,但是收盤卻飆升至150,漲幅達到7.3%。根據統計,當天的交易量為1639手合約,名義交易量1.64億美元。
2015年6月到期的30年期國債期貨與眾不同之處在於,美國政府近期宣布在2001年至2006年發售的30年期國債期貨將不會計入價格之中。休斯頓大學金融教授Craig Pirrong表示,“如此大幅的波動實屬罕見。通常來說,7.3%的漲跌可能需要幾周才能完成。我懷疑有些交易員使用了未在統計範圍內的數據,錯誤的交易模型引發了價格的扭曲。當然,我不希望自己是那個倒黴蛋。”
隔夜第一筆交易出現在美東時間11:17,價格是141.375美元;當時2015年3月的期貨價格為140.91美元,兩者十分接近。但是一位不願透露姓名的交易員表示,根據隱含價值來看的話, 2015年6月到期的合約價格應該價值151美元。
Newedge USA LLC利率策略師David Robin認為負責30年期國債期貨交易的CME集團負有一定的責任。Robin表示,“交易所應該意識到如果因為調整計價基準而出現價格非正常波動的話,他們理應采取措施並調整價格。市場需要一個公平、高效並且透明的交易環境。”
CME集團並未對此做出置評。
(更多精彩財經資訊,點擊這里下載華爾街見聞App)
數學大牛們,快到這些高薪職業碗里來!
來源: http://wallstreetcn.com/node/210432中國最好的金融求職培訓:見聞學堂(微信號:top-elites)
如果數字、數據或電子表格對你而言都是小菜一碟,那就大方秀出你的技能來吧!事實證明,做一名“數學極客”可是相當賺錢的。
來自PayScale的最新官方薪資報告數據顯示,數學專業畢業生的薪資中值在70900美元——相比之下,其他專業畢業生的薪資中值僅為58600美元。而某些職業,如數據科學家和定量分析師,其工資中值甚至可以高達10萬美元以上。
“數學極客”們完全可以憑借自己的專業技能來找到最賺錢的工作。PayScale調查了從業5-8年的數學專業畢業生的薪資水平,並列出了適合數學大牛的十大最賺錢職業:
|
排名 |
職業 |
薪資中值 |
數學專業占比 |
基本學歷 |
|
1 |
數據科學家(Data Scientist),IT |
$109,700 |
8% |
本科 |
|
2 |
定量分析師(Quantitive Analyst) |
$103,300 |
14% |
碩士 |
|
3 |
保險精算師(Actuary) |
$97,900 |
33% |
本科 |
|
4 |
數據建模工程師(Data Modeler) |
$91,200 |
18% |
碩士 |
|
5 |
高級精算分析師(Senior Actuarial Analyst) |
$86,600 |
40% |
本科 |
|
6 |
統計員(Statistician) |
$82,200 |
11% |
碩士 |
|
7 |
數學家(Mathematician) |
$81,700 |
70% |
碩士 |
|
8 |
市場調查分析師(Research Analyst), 操作分析師(Operations) |
$81,700 |
10% |
碩士 |
|
9 |
數據分析師(Statistical Analyst) |
$74,700 |
11% |
本科 |
|
10 |
精算分析師(Actuarial Analyst) |
$73,800 |
27% |
本科 |
更多精彩,請關註“見聞學堂”微信公眾號:搜索微信號top-elites,或者掃一掃
查看更多“見聞學堂”文章,請點擊右邊傳送門
(更多精彩財經資訊,點擊這里下載華爾街見聞App)
大量閱讀背誦 謝金河掌握國際趨勢 每天抄關鍵5數字 數學中段班變財經大師(118-119)
| ||||||
《今周刊》發行人謝金河透過閱報、抄筆記,以及每天看五個關鍵數字的習慣,讓他從一個數學不好的學生,蛻變成能抓住國際市場脈動的財經趨勢大師。 撰文‧鄧麗萍 無論是寫文章、演講或主持節目,謝金河對於各種總體經濟、股市重大事件、企業營運等關鍵數據如數家珍,對「數字」有超強記憶力。 但讓人跌破眼鏡的是,其實謝金河並非天生的數學高手。 「我數學從來沒有好過!」謝金河回想起在政大企管系修會計學時,從初會到管理會計、成本會計,每個學期考試都僅六十五分,低空飛過。熱中於政治和社會批判的他,在《財訊》雜誌工作的初期,對股市也是興趣缺缺。 由於工作所需,謝金河必須接觸股票,加上當時正撰寫碩士論文,靈機一動,以「台灣證券發展史」為題,到圖書館把《經濟日報》、《工商時報》舊報紙翻出來,從台股一九六二年開市看起,讀完之後,不僅嫻熟台灣證券發展史,也打通投資的任督二脈。 寫出夠力文章 台股收盤就動筆,累積十多年功力「對數字精準,能讓你更有效率。」二十多年來,謝金河投資眼光精準,累積高額資產,靠的就是閱讀各種數據,培養出對數字的超強記憶力和詮釋力。 每天早上起床,謝金河會先花半小時看美國CNBC(消費者新聞與商業頻道)新聞,再把彭博的資料看一遍,掌握所有重要的財經數據、做好筆記。其中必看五個關鍵數字,包括美元指數、道瓊指數、美國公債殖利率、油價、金價。 「有了這些背景資料,看新聞就知道怎麼回事了。」謝金河舉例,最近看到新加坡海峽時報指數收在三一六七點,他覺得似曾相識,去查資料發現,二○一三年最後一個交易日收在三一六七.○八點,再看一二年最後一天收盤,竟也是同樣的數字,「三一六七是新加坡的魔術數字」,這意味著新加坡股市連續三年都停在原地。 謝金河表示,每天持續觀察,心中就會有個基準數字,當它出現變化時,就能注意到。他打個比方說,過去上海交易所每日成交量僅五百多億元人民幣,但七月起交易量卻驟增至二千多億元人民幣。 「從量的變化,可以看出很多趨勢。」謝金河當時判斷,中國股市因「滬港通」的政策利多而熱絡起來,成交量是先行指標。果不其然,陸股在三個月內上漲逾一六%,讓他抓住中國股市上漲的契機。 剪報蒐集資訊 挖掘股票飆漲線索,培養數字詮釋力由此可見,單靠數字的記憶力,還不是投資的致勝關鍵,更重要的是,詮釋數字的能力。 如今,謝金河能夠背誦的台股代號有一千家以上,港股至少三百多家,陸股也記得二百多家。他說,今天若要查一家上市公司的財務數字,個股代號一輸入,資料就出來了。相反的,如果代號記不住,需要搜尋,就會增加一次在谷歌(Google)首頁上的時間。當資料數量很大時,浪費的時間就很可觀。 三十五歲那年,謝金河已是《財訊》月刊總編輯,同時在《財訊快報》撰寫主筆室專欄,每天寫約三千字。打從大學時代就和謝金河在社團並肩作戰的《今周刊》社長梁永煌形容,「到現在為止,台灣寫稿比老謝(謝金河)多的人,應該不多了。」謝金河勤於寫稿,中午沒吃飯,台股收盤就開始寫,一寫就十多年,在當年就已經是「喊水會結凍」的文章。 被問到三十五歲前,應該要養成哪些習慣時,謝金河認為,「起碼要喜歡閱讀。」為了做投資功課,他天天看雜誌、報紙,挖掘出哪些股票可能會漲的線索。此外,他還習慣剪報,蒐集重要資訊,坐在他辦公室旁的祕書林欣慧說,經常聽到剪報的「咔嚓」聲。 不僅如此,謝金河一邊看報,一邊在筆記本或A4紙,寫下滿滿的數字。他說,數字一定要常寫、常用,才會記得牢。「當我們把數字寫下來,透過腦袋組織解讀,數字就變得有意義。」對謝金河而言,投資的最大樂趣在於研究公司,因此,他不做金融操作如期貨或選擇權。他認為,「投資最忌卯足全力。」當槓桿控制得宜,股票下跌就下跌,只是多賺少賺,但如果連老本都押下去,風險會變得非常高。 謝金河表示,沒有人是天生的投資好手,能掌握股市脈動、趨吉避凶,祕訣在於反覆練習。他分享,以前他看到群眾都會兩腿發軟,現在演講成家常便飯。一路走來,靠的是日復一日的練習。「沒有人一開始就很棒的,都是慢慢養地成習慣。」 謝金河 出生:1957年 現職:《今周刊》發行人、財信傳媒董事長經歷:《財訊》月刊總編輯學歷:政大東亞所碩士、政大企管系 謝金河的習慣祕密檔案 好習慣:每天上班前閱讀半小時難關:經常被寫稿、開會等事務纏身養成祕訣:瀏覽關鍵數字,再手抄一遍,增強記憶力帶來最大效益:掌握市場脈動、投資眼光精準 | ||||||
數學之美番外篇:平凡而又神奇的貝葉斯方法(一) stone
來源: http://blog.sina.com.cn/s/blog_60dce3cd0100in1p.html【轉自劉未鵬博客】
概率論只不過是把常識用數學公式表達了出來。
——拉普拉斯
記得讀本科的時候,最喜歡到城里的計算機書店里面去閑逛,一逛就是好幾個小時;有一次,在書店看到一本書,名叫貝葉斯方法。當時數學系的課程還沒有學到概率統計。我心想,一個方法能夠專門寫出一本書來,肯定很牛逼。後來,我發現當初的那個樸素歸納推理成立了——這果然是個牛逼的方法。
——題記
目錄
0. 前言
1. 歷史
2. 拼寫糾正
3. 模型比較與貝葉斯奧卡姆剃刀
4. 無處不在的貝葉斯
5. 樸素貝葉斯方法(又名“愚蠢者的貝葉斯(idiot’s bayes)”)
6. 層級貝葉斯模型
7. 貝葉斯網絡
0.
這是一篇關於貝葉斯方法的科普文,我會盡量少用公式,多用平白的語言敘述,多舉實際例子。更嚴格的公式和計算我會在相應的地方註明參考資料。貝葉斯方法被證明是非常 general 且強大的推理框架,文中你會看到很多有趣的應用。
1.
托馬斯·貝葉斯(Thomas Bayes)同學的詳細生平在這里。以下摘一段 wikipedia 上的簡介:
所謂的貝葉斯方法源於他生前為解決一個“逆概”問題寫的一篇文章,而這篇文章是在他死後才由他的一位朋友發表出來的。在貝葉斯寫這篇文章之前,人們已經能夠計算“正向概率”,如“假設袋子里面有N個白球,M個黑球,你伸手進去摸一把,摸出黑球的概率是多大”。而一個自然而然的問題是反過來:“如果我們事先並不知道袋子里面黑白球的比例,而是閉著眼睛摸出一個(或好幾個)球,觀察這些取出來的球的顏色之後,那麽我們可以就此對袋子里面的黑白球的比例作出什麽樣的推測”。這個問題,就是所謂的逆概問題。
實際上,貝葉斯當時的論文只是對這個問題的一個直接的求解嘗試,並不清楚他當時是不是已經意識到這里面包含著的深刻的思想。然而後來,貝葉斯方法席卷了概率論,並將應用延伸到各個問題領域,所有需要作出概率預測的地方都可以見到貝葉斯方法的影子,特別地,貝葉斯是機器學習的核心方法之一。這背後的深刻原因在於,現實世界本身就是不確定的,人類的觀察能力是有局限性的(否則有很大一部分科學就沒有必要做了——設想我們能夠直接觀察到電子的運行,還需要對原子模型爭吵不休嗎?),我們日常所觀察到的只是事物表面上的結果,沿用剛才那個袋子里面取球的比方,我們往往只能知道從里面取出來的球是什麽顏色,而並不能直接看到袋子里面實際的情況。這個時候,我們就需要提供一個猜測(hypothesis,更為嚴格的說法是“假設”,這里用“猜測”更通俗易懂一點),所謂猜測,當然就是不確定的(很可能有好多種乃至無數種猜測都能滿足目前的觀測),但也絕對不是兩眼一抹黑瞎蒙——具體地說,我們需要做兩件事情:1. 算出各種不同猜測的可能性大小。2. 算出最靠譜的猜測是什麽。第一個就是計算特定猜測的後驗概率,對於連續的猜測空間則是計算猜測的概率密度函數。第二個則是所謂的模型比較,模型比較如果不考慮先驗概率的話就是最大似然方法。
1.1
下面舉一個自然語言的不確定性的例子。當你看到這句話:
The girl saw the boy with a telescope.
你對這句話的含義有什麽猜測?平常人肯定會說:那個女孩拿望遠鏡看見了那個男孩(即你對這個句子背後的實際語法結構的猜測是:The girl saw-with-a-telescope the boy )。然而,仔細一想,你會發現這個句子完全可以解釋成:那個女孩看見了那個拿著望遠鏡的男孩(即:The girl saw the-boy-with-a-telescope )。那為什麽平常生活中我們每個人都能夠迅速地對這種二義性進行消解呢?這背後到底隱藏著什麽樣的思維法則?我們留到後面解釋。
1.2
貝葉斯公式是怎麽來的?
我們還是使用 wikipedia 上的一個例子:
一所學校里面有 60% 的男生,40% 的女生。男生總是穿長褲,女生則一半穿長褲一半穿裙子。有了這些信息之後我們可以容易地計算“隨機選取一個學生,他(她)穿長褲的概率和穿裙子的概率是多大”,這個就是前面說的“正向概率”的計算。然而,假設你走在校園中,迎面走來一個穿長褲的學生(很不幸的是你高度近似,你只看得見他(她)穿的是否長褲,而無法確定他(她)的性別),你能夠推斷出他(她)是男生的概率是多大嗎?
一些認知科學的研究表明(《決策與判斷》以及《Rationality for Mortals》第12章:小孩也可以解決貝葉斯問題),我們對形式化的貝葉斯問題不擅長,但對於以頻率形式呈現的等價問題卻很擅長。在這里,我們不妨把問題重新敘述成:你在校園里面隨機遊走,遇到了 N 個穿長褲的人(仍然假設你無法直接觀察到他們的性別),問這 N 個人里面有多少個女生多少個男生。
你說,這還不簡單:算出學校里面有多少穿長褲的,然後在這些人里面再算出有多少女生,不就行了?
我們來算一算:假設學校里面人的總數是 U 個。60% 的男生都穿長褲,於是我們得到了 U * P(Boy) * P(Pants|Boy) 個穿長褲的(男生)(其中 P(Boy) 是男生的概率 = 60%,這里可以簡單的理解為男生的比例;P(Pants|Boy) 是條件概率,即在 Boy 這個條件下穿長褲的概率是多大,這里是 100% ,因為所有男生都穿長褲)。40% 的女生里面又有一半(50%)是穿長褲的,於是我們又得到了 U * P(Girl) * P(Pants|Girl) 個穿長褲的(女生)。加起來一共是 U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl) 個穿長褲的,其中有 U * P(Girl) * P(Pants|Girl) 個女生。兩者一比就是你要求的答案。
下面我們把這個答案形式化一下:我們要求的是 P(Girl|Pants) (穿長褲的人里面有多少女生),我們計算的結果是 U * P(Girl) * P(Pants|Girl) / [U * P(Boy) * P(Pants|Boy) + U * P(Girl) * P(Pants|Girl)] 。容易發現這里校園內人的總數是無關的,可以消去。於是得到
P(Girl|Pants) = P(Girl) * P(Pants|Girl) / [P(Boy) * P(Pants|Boy) + P(Girl) * P(Pants|Girl)]
註意,如果把上式收縮起來,分母其實就是 P(Pants) ,分子其實就是 P(Pants, Girl) 。而這個比例很自然地就讀作:在穿長褲的人( P(Pants) )里面有多少(穿長褲)的女孩( P(Pants, Girl) )。
上式中的 Pants 和 Boy/Girl 可以指代一切東西,所以其一般形式就是:
P(B|A) = P(A|B) * P(B) / [P(A|B) * P(B) + P(A|~B) * P(~B) ]
收縮起來就是:
P(B|A) = P(AB) / P(A)
其實這個就等於:
P(B|A) * P(A) = P(AB)
難怪拉普拉斯說概率論只是把常識用數學公式表達了出來。
然而,後面我們會逐漸發現,看似這麽平凡的貝葉斯公式,背後卻隱含著非常深刻的原理。
2.
經典著作《人工智能:現代方法》的作者之一 Peter Norvig 曾經寫過一篇介紹如何寫一個拼寫檢查/糾正器的文章(原文在這里,徐宥的翻譯版在這里,這篇文章很深入淺出,強烈建議讀一讀),里面用到的就是貝葉斯方法,這里我們不打算複述他寫的文章,而是簡要地將其核心思想介紹一下。
首先,我們需要詢問的是:“問題是什麽?”
問題是我們看到用戶輸入了一個不在字典中的單詞,我們需要去猜測:“這個家夥到底真正想輸入的單詞是什麽呢?”用剛才我們形式化的語言來敘述就是,我們需要求:
P(我們猜測他想輸入的單詞 | 他實際輸入的單詞)
這個概率。並找出那個使得這個概率最大的猜測單詞。顯然,我們的猜測未必是唯一的,就像前面舉的那個自然語言的歧義性的例子一樣;這里,比如用戶輸入: thew ,那麽他到底是想輸入 the ,還是想輸入 thaw ?到底哪個猜測可能性更大呢?幸運的是我們可以用貝葉斯公式來直接出它們各自的概率,我們不妨將我們的多個猜測記為 h1 h2 .. ( h 代表 hypothesis),它們都屬於一個有限且離散的猜測空間 H (單詞總共就那麽多而已),將用戶實際輸入的單詞記為 D ( D 代表 Data ,即觀測數據),於是
P(我們的猜測1 | 他實際輸入的單詞)
可以抽象地記為:
P(h1 | D)
類似地,對於我們的猜測2,則是 P(h2 | D)。不妨統一記為:
P(h | D)
運用一次貝葉斯公式,我們得到:
P(h | D) = P(h) * P(D | h) / P(D)
對於不同的具體猜測 h1 h2 h3 .. ,P(D) 都是一樣的,所以在比較 P(h1 | D) 和 P(h2 | D) 的時候我們可以忽略這個常數。即我們只需要知道:
P(h | D) ∝ P(h) * P(D | h) (註:那個符號的意思是“正比例於”,不是無窮大,註意符號右端是有一個小缺口的。)
這個式子的抽象含義是:對於給定觀測數據,一個猜測是好是壞,取決於“這個猜測本身獨立的可能性大小(先驗概率,Prior )”和“這個猜測生成我們觀測到的數據的可能性大小”(似然,Likelihood )的乘積。具體到我們的那個 thew 例子上,含義就是,用戶實際是想輸入 the 的可能性大小取決於 the 本身在詞匯表中被使用的可能性(頻繁程度)大小(先驗概率)和 想打 the 卻打成 thew 的可能性大小(似然)的乘積。
下面的事情就很簡單了,對於我們猜測為可能的每個單詞計算一下 P(h) * P(D | h) 這個值,然後取最大的,得到的就是最靠譜的猜測。
一點註記:Norvig 的拼寫糾正器里面只提取了編輯距離為 2 以內的所有已知單詞。這是為了避免去遍歷字典中每個單詞計算它們的 P(h) * P(D | h) ,但這種做法為了節省時間帶來了一些誤差。但話說回來難道我們人類真的回去遍歷每個可能的單詞來計算他們的後驗概率嗎?不可能。實際上,根據認知神經科學的觀點,我們首先根據錯誤的單詞做一個 bottom-up 的關聯提取,提取出有可能是實際單詞的那些候選單詞,這個提取過程就是所謂的基於內容的提取,可以根據錯誤單詞的一些模式片段提取出有限的一組候選,非常快地縮小的搜索空間(比如我輸入 explaination ,單詞里面就有充分的信息使得我們的大腦在常數時間內把可能性 narrow down 到 explanation 這個單詞上,至於具體是根據哪些線索——如音節——來提取,又是如何在生物神經網絡中實現這個提取機制的,目前還是一個沒有弄清的領域)。然後,我們對這有限的幾個猜測做一個 top-down 的預測,看看到底哪個對於觀測數據(即錯誤單詞)的預測效力最好,而如何衡量預測效率則就是用貝葉斯公式里面的那個 P(h) * P(D | h) 了——雖然我們很可能使用了一些啟發法來簡化計算。後面我們還會提到這樣的 bottom-up 的關聯提取。
投資的數學題(三) 許渺
來源: http://xueqiu.com/1460633374/35816323去年寫了兩篇《投資的數學題(一)(二)》(鏈接附在下面),沒想到雪球關註度挺高,甚至微信到處都是轉發,有幾次我身邊的朋友不知道從哪里來的公眾號轉發到朋友圈,著實嚇了我一跳,今天奉上《投資的數學題(三)》,希望能幫助大家換一個角度去思考投資這件事情,
一、關於投資成功的概率
如果你投資成功的概率是60%,那麽意味著你連續投資100次,其中60次盈利,40次虧損。如果你把止盈和止損都設置為10%和-10%,那麽意味著最終的收益率是350%(1.1^60*0.9^40=4.50)
解讀:是的,小夥伴,已經亮瞎你的眼了吧,3.5倍的收益率!而接下來你需要思考的是你怎麽能保證你的勝率是60%吶,不要想當然,這個成功率對於多數人來說也是幾乎不可能達到的。(註:飛機上臨時寫的,由於函數設置錯誤,謝謝@哞哞嗷嗷 @長風半日 @ddoer 三位球友指正,已修改)
二、關於止盈止損
索羅斯說過他不在乎勝負的概率,而期望盈利的時候比虧損時候能多賺一些。假設我們每次止盈是10%,每次止損是-5%,那麽連續投資100次,假設勝負概率是50%,那麽意味著你最終的收益率是803.26%(1.1^50*0.95^50=9.0326)
解讀:是的,你沒有看錯,收益率是800%。前提是你可以堅決的止損和止盈,其次你能保證50%的概率能到達更多的止盈機會嗎?
三、關於正態分布
這個世界上很多事物都呈現正態分布,比如天才和蠢蛋的比例很少,多數的庸庸碌碌的大眾,也比如社會財富的分配,富人和窮人也呈現正態分布,人類的身高、體重等等太多的事物都呈現正態分布。無論牛熊市,所有股票的漲跌幅和大盤相比也會呈現正態分布,能沅超越指數上漲的股票最終只是少數。當你想取得超額的時候,一定是你某項因素或是某項能力也同樣達到了正太分布的那偏正的極小區域。如果你沒有這樣能力,該怎麽辦吶?當然了,命好是投資的核心競爭力,但不要忘記,命運好壞也會是正態分布的。
四、關於馬太效應
土豪賬戶1億元本金,屌絲賬戶10萬元本金,土豪一年收益10%,屌絲一年收益率100%。年底時土豪賬戶1.1億元,屌絲賬戶20萬元,雙方差距又拉大了990萬元。當你的本金和別人不是一個數量級時,你很可能並不知道對方是怎麽想的。
五、雞和兔子的數學題
問雞和兔子18只,一共46條腿,問雞多少只?兔子多少只?
解讀:常規的思考方式是雞為X,然後兔子是18-X,在設一元方程求解。而超凡的思維是讓所有雞和兔子都擡起兩條腿,這樣一共擡起18*2=36條腿,還剩下10條腿都是兔子的,因此兔子是5只,雞有13只。所以你要相信在同樣的股價數據面前,有些人是和你思考方式完全不一樣的。
六、關於穩健投資
投資者A和B,A取得連續兩年收益第一年10%,第二年50%,B保持了兩年每年30%的收益率,問兩年後誰的收益率高。
解讀:結果是B兩年69%的收益率高於A兩年65%,高出了4個百分點,很簡單的一道題只為告訴大家穩健投資不等於低收益,而是為了保證最終獲得更高收益率的確定性更強。
七、關於交易頻率
按照傭金萬五,印花稅千一計算,一年10倍的換手率,意味著交易成本是(0.05%*2+0.1%)*10=2%。當對於每周就要大換倉的小夥伴們,一年的交易成本已經超過了10%,你還沒有借到杠桿資金,去付出了比杠桿資金更高的資金成本。Nuo zuo nuo die,除非你有強大的獲利本領,否則降低你的交易頻率,要不然你會把股市的平均收益都捐給券商和政府。
八、關於量化投資
所謂量化投資就是建模型,導數據,控制風險,自動交易。更恰當的比喻是找對象這件事情,我們自己做的多數是定性投資,包括兩個流派:基本面分析和技術分析。前者參考教育、收入、家庭、性格諸多因素,然後挖掘白馬大藍籌,長期持有一輩子,後者如今越來越流行,因為這就是個看臉和feel的年代。而父母在這件事情往往是堅定不移的“量化投資者”,他們限定了本地戶口、經濟寬綽、父母健康、人品良好、有住房(大於100平米無貸款)、離婚喪偶直接OUT等等的一系列指標,然後賦予不同的權重,當滿足條件的時候便會積極的要求執行交易。至於那種方式能夠幸福吶?見仁見智吧。唯一的區別量化可以高頻交易,結婚這件事最好就一次。
學了7年量化投資,做了7年量化交易,醒悟了8個字”不虧、穩健、持續、長期”就是王道。人生就是個複利的過程,最後能得到什麽,取決於前面積累了什麽。努力做個+∞的人。
附鏈接:
《投資的數學題(一)》http://xueqiu.com/1460633374/26859259
《投資的數學題(二)》http://xueqiu.com/1460633374/26875591
某量化賬戶數據(截止2013年12月10日)
(註:這個賬戶是2008年8月開始進行的量化交易,初始本金380萬元,目前市值1530萬元,折合年化收益率24%,此賬戶僅進行極大概率事件的量化投資,目前沒有任何虧損股票案例)
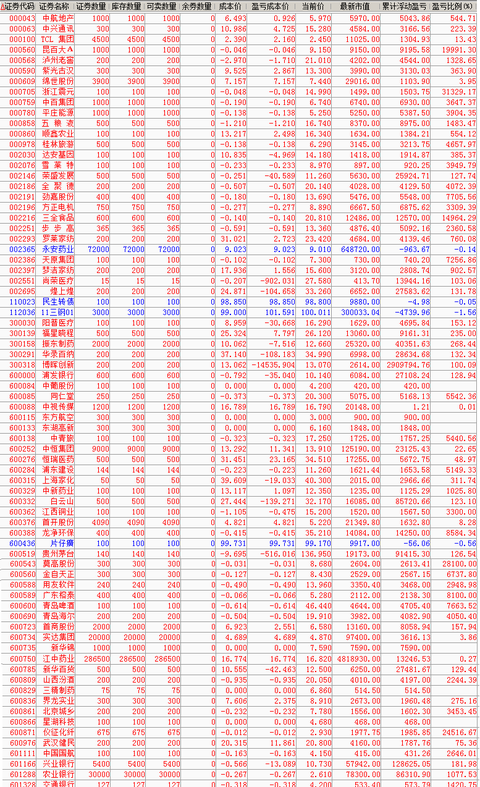
@小小辛巴 @方舟88 @黃金的十月 @七向街 @O_Livia @DAVID自由之路 @唐小帥 @東博老股民 @蘑菇樹 @userfield @不明真相的群眾 @不明覺厲的小夥伴 @steven_愛股
蜘蛛俠爸爸的天才數學方程式 朱泙漫屠龍記
http://johnchrysostom.blogspot.hk/2015/04/blog-post.html除了數學、統計 也招募企管、行銷人才 大數據挖礦人 未來職場最搶手
2015-07-20 TWM
|
「哪一種職業是二十一世紀最性感的職業?」答案與外貌無關。他們是一群一向隱身在大數據背後,每天花上整天時間與數據及資料相處,從數據中挖掘價值的人,他們是數據科學家,是你不能不知道的明日之星職業。 撰文•周品均 試想,一部電影還沒開拍前,就能準確預測它上映後的票房;兒童腸病毒疫情爆發前,家長能提早幾天知道這個疫情將爆發的狀況。這些過去做不到的精準預測,如今都靠著「大數據(Big Data)」一一實現了。 要能精準預測,靠的可不只是大數據的運算工具,還有隱身在數據背後的祕密功臣——數據科學家(Data Scientist)。 數據科學家是誰?是精通數學領域的科學家?還是會寫程式的工程師?答案可以都是,也可以都不是。數據科學家是具備開鑿資料深山的能力與耐心、同時又能透過演算法在巨量資料中找到價值的人。 這些運用大數據工具,每日與大數據為伍,目標就是在數據中挖掘到寶藏的人,不只有著「數據科學家」這個酷炫職稱,甚至有「二十一世紀最性感職業」的職稱。 須跨領域能力 人才供不應求不僅如此,數據科學家供不應求。「這類人才很缺,要找人很不容易。」大數據軟體公司TERADATA大數據事業部高級顧問王隆生透露。 數據科學家這項職業,在人力市場的供需缺口有多大,從麥肯錫報告就能略知一二。麥肯錫的調查指出,光是美國地區,數據分析專才的缺口高達十四萬到十九萬名。打開專業社群網站LinkedIn,搜尋數據科學家職缺,光是美國地區就有超過三萬筆。 台灣對於這項新興職業的需求也已悄然浮現,一○四人力銀行總經理洪廣禮強調,新興職缺例如資料科學家、數據洞察分析師、物聯網智能研發工程師需求火紅。無 論是在一○四求職平台上,或是LinkedIn的平台上搜尋數據科學家的相關職缺,不難發現開出數據分析師職缺的公司已不再是大數據公司或是軟體公司,像 是華碩、台達電等製造業,或是電信公司、金融業等也都紛紛開出數據科學家的職缺。 看到這裡,你是否好奇,若想做這份二十一世紀最性感職業,究竟需要哪些能力呢?國內知名輿情分析公司意藍科技董事總經理楊立偉解答:「這是個跨領域的職 業,除了對資訊科技(電腦)的熟悉,還要熟悉數學、統計等資料處理方法,以及對不同領域(產業)的熟悉。」這三項專業知識橫跨不同學院學科,包括解電腦操 作、程式撰寫的理工科系,以及懂得資料處理方法的統計與數學科系,同時還要不同領域的專家,像是行銷學系、公共衛生學系、大眾傳播學系專才。 不可否認的是,要找到同時能專精寫程式、又深諳資料處理方法,還要非常懂特定產業或領域的人才,簡直是不可能。「其實數據科學家多半是一個團隊。」楊立偉與王隆生不約而同地表示。 雖然都是組建大數據團隊,但位於不同產業位置的公司,對數據科學家團隊需求的專業能力與特質也有所不同。TERADATA提供從專業數據倉儲、處理到數據 分析解決方案,也因此,數據科學家團隊多從資料處理角度去思考,目標做出能完美預測的模型。王隆生表示,當他在招募數據科學家人才時,他看中對方懂不懂統 計以及機器學習,同時要具備寫程式的能力,「你不能只用講的,然後在紙上推導。」他強調。 但反觀意藍科技提供的是蒐集、處理、分析各類型網路資訊與情報的服務,更需要從人的角度去思考。這也是為什麼楊立偉認為:「成為數據科學家的三個條件中, 其實領域專家是最重要的。」楊立偉解釋,年輕世代很早就接觸電腦,對於資訊工具的使用並不陌生,現在也有很多免費的工具可以使用,甚至是統計能力也都可以 找到免費資源補強,重要的是當你有了工具與材料,你要怎麼用它,而這就是領域專家的重要性。 「我都稱他們(數據科學家)為小偵探。」楊立偉說,我帶你進入一個布滿卷宗的資料室,給了你一支手電筒,那你要看什麼,或是看什麼是有價值的,這就考驗著你「命題」的能力。 必備好奇心、資料嗅覺 例如,來自公衛系的數據科學家,從特定疾病傳播進行命題,找到有價值的資料;傳播學系、政治系等從其專業下去命題,「以前都在電機、資訊、資管找人,現在我會到圖資系、管理學院、行銷企管等系所找尋人才。」楊立偉透露。 儘管,隨著公司提供的產品與服務不同,對數據科學家不同專業能力的看中程度不一,不過幾項專家眼中稱職的數據科學家須具備的特質,仍值得有志從事大數據領域的人參考。 首先是敏銳的資料嗅覺。數據科學家每天與數據為伍,「是的,大部分時間,小偵探們都是坐在電腦前面對數據。」楊立偉笑說。王隆生也以自身經驗分享,有的時候客戶不會先提供數據,數據科學家就要先在網路找資訊,透過資料嗅覺,預先判斷出一些資訊。 其次是好奇心,「你要對數據背後代表的意義感到好奇,對於資料能夠做什麼事情感到好奇。」王隆生分析。另外,數據科學在處理與分析數據時,有時會出現自己 認為做出來的結果顯著,符合命題,但卻沒有將產業的常態狀況考慮進去,導致偏誤,也因此,避免認知偏誤也是數據科學家應該要努力的方向。 當然還有團隊合作能力,就拿TERADATA的數據科學家團隊來說,大中華地區成員就有二十三位、意藍科技的數據科學家成員則有二十至三十位。 如果想加入這二十一世紀最夯的職業,該要如何培養相關能力?「以前大家常說,知識就是力量,現在變成資料就是力量。」楊立偉直言,過去兩年人類所產生的數據占了人類歷史上數據總量九成,也就是數據急速成長,以後各行各業都需要與數據為伍的人。 新手待遇 年薪可達百萬他建議:「及早培養解讀數據的能力。」包括使用統計軟體,在專業領域中建立命題能力,找尋數據價值尤為重要。 王隆生則認為,數據科學家的能力要從在學時就培養,他建議未來想要從事大數據領域的青年學子,應該要在大學時,修習統計、微積分、線性代數等學科,將基礎學科的根基打好。也可以從就學時,透過參與老師的專案研究,先行累積對產業的認識。 大數據正夯,數據科學家供不應求,反映在高薪待遇,專家透露,一位新手就有百萬年薪的待遇。想加入這項未來數年高含金量工作行列,提前培養相關能力不可少。 數據科學家錢景一片光明 ——2015年美國10大最佳工作 職業 就業 增長率 (%) 平均 年收入(美元) 數據科學家 14.97 $124,149 數學家 25.91 $102,182 精算師 25.09 $94,209 軟體工程師 21.13 $93,113 生物醫學工程師 26.65 $89,165 電腦分析工程師 23.50 $81,150 統計學家 25.91 $79,191 職能治療師 29.14 $77,114 聽力學家 33.33 $71,133 牙科保健師 31.02 $71,102 註:數據科學家是跨領域的職業,要熟悉數學、統計等資處方法資料來源:CareerCast |
||
談《交易的數學》 - 賺回的幾何級遞增系數
關鍵人物》對自己殘忍、對客戶仁慈的傳奇CEO 一個數學老師 變身全球線上影音之王
網飛共同創辦人暨執行長哈斯汀(Reed Hastings)在創業時,把數學運用在公司經營。不管同事、對手或自己,不符合其方程式者一律刪除。「理性的殘忍」,正是信奉數學邏輯的哈斯汀最大特色。 出身數學世家 外曾祖父的實驗室催生網路和雷達 哈斯汀的家族和數學早有淵源。他的外曾祖父盧米斯(Alfred Lee Loomis)靠其數學天賦,在一九二九年美國股災中獲利。盧米斯致富後成立了一個實驗室,廣邀全球最傑出科學家研發軍事應用,為後來的原子彈、雷達和全球定位系統打下基礎。美國聯邦政府成立的「國防先進研究計畫署」(DARPA),就是源自盧米斯的實驗室,該單位後來開發出全球資訊網(world wide web),就是網路的前身。 繼承家族數學天賦的哈斯汀,大二時就獲得高等數學榮譽獎,大學畢業後加入和平部隊,奉派到非洲史瓦濟蘭教數學。一九九一年,哈斯汀創辦軟體公司「純粹」(Pure)。隨著公司員工逐漸從十人成長到六百四十人,「我覺得我已跟不上腳步,腦袋一片空白。」董事會要他擔任執行長,他自我檢討:「我做得實在不怎麼樣。」最後他要求董事會將他解雇,「我炒我自己魷魚,而且是兩次。」 對老戰友不留情公司利益第一,裁他前資遣費早算好 哈斯汀對待老戰友也是同樣的標準。藍道夫(Marc Randolph)和哈斯汀後來一起創立網飛。不過,當時哈斯汀的興趣轉向教育與政治,真正將網飛概念落實的,其實是藍道夫。 後來哈斯汀重拾對網飛的興趣,他一回到公司不久,就在某次公開會議上,當眾宣布他要和藍道夫擔任共同執行長。藍道夫臉色頓時慘白,與會者發現,哈斯汀根本事先沒和藍道夫討論過。哈斯汀隨後轉向藍道夫聘用的人資經理,當場將其解雇,讓在場同事目瞪口呆。 在哈斯汀成為公司主導者後,藍道夫有意將自己定位在產品開發,然而哈斯汀後來卻將這份工作分配給技術長,要藍道夫去測試一個自動租片機的點子。「若這次測試失敗會怎樣?」藍道夫問。「那你就得離開這家公司。」哈斯汀在回答之時,藍道夫甚至發現他已擬好了資譴條件。 《富比世》專欄記者基廷(Gina Keauing)形容哈斯汀:「堅定不移要求自己的員工做到最好,並以公司利益來行事。」哈斯汀不在乎人情世故,他聘請麥卡錫(BarryMcCarthy)為財務長,看重其市場眼光敏銳,麥卡錫也被視為哈斯汀接班人。不過後來哈斯汀又聘用基爾戈(Leslic Kilgore)主管行銷,在一次董事會上,哈斯汀當著麥卡錫的面,公開說他心目中接班人是基爾戈,讓麥卡錫一臉尷尬。 有些主管會對下屬搞「恐怖平衡」之類的帝王心術,哈斯汀不搞這一套,他只有「誰適合做什麼」的理性分析。如基廷所說:「哈斯汀把公司比喻成一個專業球隊,球員只能靠業績贏得上場比賽的時間。」當員工在哈斯汀的數學方程式裡沒有作用,下場就是被刪除。 二〇〇一年九月,網飛首次公開募股前夕,為改善公司財務狀況,哈斯汀決定親自裁員。他要所有員工立刻到公司中庭,當眾宣布若要打敗競爭者,網飛須削減成本:「這就是今天局面,你們有很多人會失去工作,我對此很遺憾。」那天結束時,網飛有四成員工遭解雇。 對敵人更狠心建財務模型,「算」對手債務違約死期 哈斯汀還把數學分析套用到對手身上。二〇〇四年,百視達決定和網飛打價格戰,消息一出讓網飛股價暴跌。哈斯汀立刻開啟他的數學模式:由財務長領軍,利用公司建立的訂戶指標,為百視達的線上及門市業務建立財務模型,測算價格戰對百視達資產負債表的影響。 經過數學推算,財務人員告訴哈斯汀,他們完全確定百視達會在何時終止價格戰,否則就會債務違約。當時市場一面倒看衰網飛,華爾街大量做空網飛股票,該公司將被收購傳聞不絕,但哈斯汀對數學模型深具信心,不斷澄清市場傳言。 他的堅持有了回報:隔年市場開始擔心百視達債務攀升,惠譽(Fitch)和標準普爾(S&P)把百視達的信用大幅調降為垃圾等級。二〇〇五年夏天百視達爆發財務危機,後來主動漲價,這場價格戰以網飛勝利告終,它的市值也超越百視達。他接受本刊專訪時說:「我們的成功,是基於專注在一件事,並把它做到最好。」 金庸曾說,政治人物要有兩種忍功:一是忍耐,二是殘忍,兩者的最高目標都是為奪權。信奉數學的哈斯汀深信「對消費者仁慈,就要對自己殘忍」,這是哈斯汀在市場競爭下的「適者生存」哲學,也是網飛能席捲全球一百九十國的最終之秘。 若追根究柢,網飛成事關鍵還是:制定規則能落實,不說一套做一套。這原則聽來簡單,卻是多數領導人未及之處。 撰文 楊少強 | ||||
小即使多的數學。
巴黎:這裡是一個現實的例子:
有兩支甲和乙股票,兩支資產值都是100元,所有的債,ROE都是一樣10%,本年都是賺10元,乙派息10元,甲派息2元,甲的資產淨值於是=108,乙仍然是100元。
純數學計算認為甲的股價是108元,乙應該是100元。
於是甲的PE便是10.8陪,yield是1.85%,乙的PE是10倍,yield是10%。
純數學計算認爲乙和甲的投資者的財富沒有分別。
但大家都沒有純數學家的感覺,可以說實淺經驗并不是純數學想象那樣。
例如筆者持有的互太每年的增長不高,但卻越派息,PE越高。
相似的例子記錄在BenGraham的SecurityAnalysis一書内,有興趣的朋友可以花時間研究。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
交易方面,前在低位買入的財險算是較幸運,今天升了3.5%,總共有10%+,熊市就是這樣,賺多了的企業會一起陪跌,為耐性的投資者制造機會。
另外有同學告訴我川河持有的湯臣發盈喜,其實川河的經常性物業租金收入、又兩個大股東的持貨、其持有的上市證券的股息收入相對穩定,那些額外的賣樓收入對我來說只是Bonus。但它就是因爲派息不多,股價升不起(上面說的原因),已經9年不增派下現金越來越多,還高過市值,不過每等一年,現金每增多一億,增派的機會就會越再增加,股價就越有機會大幅上升,但如不增派,它的現金也跑不掉。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
有海外朋友希望可以參加投資班,筆者決定試行海外直播教學。
Next Page





