📖 ZKIZ Archives

股票+股票 VS 股票+現金

前幾篇文章談到投資中兩種截然不同的情況，第一種，對於有edge的股票，盡可能分散地買，可以把Expected Growth推到最大；第二種，一注獨贏於盈利率與虧損度之比懸殊的股票，也能令資本的增長速度達至最快。究竟以一注獨贏之“矛”，對分散投資之“盾”，何者更優勝呢？那就帶著矛盾再研究吧。

一注獨贏好還是分散投資好，不僅是片面和主觀的方法之爭，把背後的條件和理據弄清楚、搞明白，對具體的操作也很有現實意義。如果可以順利解決什麼時候選擇“股票+現金”組合較有利，什麼時候選擇“股票+股票”組合較有利，也就可以間接回答Wanderer師弟所提出那條看似無從入手的難題：同2800做rebalance，用現金好，還是reits、公用股的組合好？

首先探討一下“股票+現金”組合，再次搬出最優化資本分配公式：
f = p/a – q/b
其中，f是投入資本的最佳比例，p是盈利的機會率；q是虧損的機會率；a是虧損幅度；b是淨盈利率。
相對應f這個比例，其最快增長速度，g = p*ln(1+f*b)+q*ln(1-f*a)

為了方便比較，選用上文例子中股票A的條件，假設輸贏概率都是固定的（例子中都是0.5），expected value也是固定的（例子中是0.6），這樣，就可以得出盈利率與虧損幅度之比對資金增長的影響了。

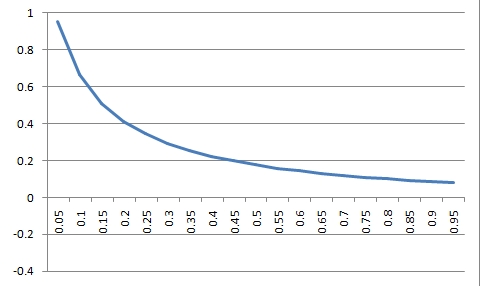
而且，因為expected value = p*b-q*a，在這個例子中p和q都為0.5，而expected value又是固定，即(b-a)是固定的，故只需考慮只其中一個變量就夠了。在一般沒經槓桿操作的賭局或股票中，虧損幅度，即a，只會處於0與1之間，所以選取a來比較會更便於解釋結果。把0<a<1代入g，就可看到“股票+現金”組合相對於虧損幅度的資金增長變化，如下圖：



現在考慮另一種選擇，“股票+股票”組合，不保留現金，把資金平均分配於兩只條件一樣但可能升跌不同步的股票A和B。同樣假設股票A和B都符合上述例子中的條件，每一輪投資不外乎四種結果：

第一種：1/4機會，A升B升，資金的收益變化是：1+0.5*b+0.5*b

第二種：1/4機會，A升B跌，資金的收益變化是：1+0.5*b-0.5*a

第三種：1/4機會，A跌B升，資金的收益變化是：1-0.5*a+0.5*b

第四種：1/4機會，A跌B跌，資金的收益變化是：1-0.5*a-0.5*a

所以，每一輪的資金增長就是：

g = 0.25*ln(1+b)+0.5*ln(1+0.5b-0.5a)+0.25*ln(1-a)

同樣把0<a<1代進去，得出“股票+股票”組合相對於虧損幅度的資金增長變化，如下圖：



想知道“矛”厲害一些，還是“盾”厲害一些，把上面兩幅圖疊起來就一清二楚了：



原來真是各有千秋，a很小，即風險很低時，一注獨贏的“股票+現金”組合（藍色線）佔盡上風；a很大，即風險很高時，也是“股票+現金”組合佔優；中度風險時，則是“股票+股票”組合（紅色線）較優。

實際操作中雖然各項參數不盡相同，但面對不同的風險程度時優化資本配置應是離不開這個大範圍的。而風險對於資本配置的影響，正正是大多數人的決策盲點。

習慣上，投資者普遍會以預期收益來主導決策，很少反過來根據風險作決策，即心存僥幸，不作最壞打算。例如收租仔加按再加按，喊一句gogogo，就以為樓價只會升不會跌；又如財演大師買完股，跳一part求雨舞（魔術師語），就幻想a=0可以不用理會。恐怕最後真是要自求多福了。
PermaLink: https://articles.zkiz.com/?id=229467
Next Page
ZKIZ Archives @ 2019