📖 ZKIZ Archives

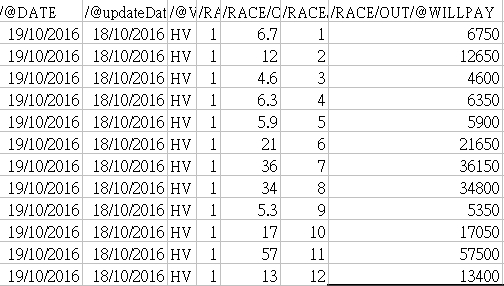
得寸進尺　從獨贏到連贏

完成計算獨贏機率的model，很自然要面對一個問題：即使計算相對準確、長線有利，但實際操作時只會下注有edge的馬匹，而非必然是機會率最大的馬匹，故勝出率不會很高，更難免會出現一個又一個擦身而過的遺憾。

真係“好o既唔靈醜o既靈”，周日一戰，四隻重注馬，“華美之友”、“嫡愛寶”、“華恩庭”和“東方快車”，三隻跑第二，一隻跑第四，如非中隻“宅大大”，獨贏投注差點就顆粒無收，掃興、冇癮。

意外的是試驗中的連贏投注表現很好，起到了失之東隅、收之桑榆的效果，不但“華美之友”、“華恩庭”、“宅大大”和“東方快車”這幾場都是正回報，（下圖為“期惑”搭“東方快車”）



連頭場獨贏投注沒有edge的“四平八穩”搭“彩球”，居然也是正回報：



構思連贏投注系統的出發點很簡單，如果計算出來的獨贏有edge，包含了獨贏機率的連贏也應該有edge，只需要思考的是，怎樣才能保證由獨贏機率推算連贏機率時不會過度偏差。

在“名次的煩惱”一文，池某曾質疑過由獨贏機會率推算位置機會率的可行性，有的馬陣上表現非贏即大敗，有的馬是place王唔識贏，獨贏與位置雖然有關係，卻非劃一的比例關係，因此池某想過不如另闢蹊徑獨立地計算位置的機會率，不過，一試之下，發覺這種想法很難成功，最大的問題，是無法保證計算結果的row sum等於1，特別是一面倒的大熱門，很容易得出位置機會率大於1的荒謬結果。

此路不通就惟有參考別人的做法了，若以可行為前提，方便為標準，最方便的可行之法還是Harville formula。Harville formula是利用條件機率（conditional probability）的計算方法，把B馬跑第二的機會率，變成當A馬不在時B馬跑第一的機會率，A馬跑第一而同時B馬跑第二的機會率就是：
p(A)*p(B)/(1-p(A))
同理，B馬跑第一而同時A馬跑第二的機會率就是：
p(B)*p(A)/(1-p(B))
於是，A馬和B馬構成的連贏機率就是：
p(A)*p(B)/(1-p(A))+ p(B)*p(A)/(1-p(B))

這裡說的方便，不僅是對了解這條公式的人而言，不了解的，同樣很方便就能使用其計算結果，外國有些網站提供online的odds calculator，只需輸入一場馬獨贏的機會率，立即就能計出每匹跑每個名次的機會率，所使用的就是Harville formula，即使不明白其背後原理，使用起來亦全無難度。

針冇兩頭利，選擇了簡單方便，就要放棄另一個重要選項──準確度。前文已經說過，Harville formula的偏差頗大，特別是在冷熱門賠率懸殊的場合。要消除偏差，又要參考別人的做法了。原來早在上世紀八九十年代，就有人指出了Harville formula的偏差，並提出修正之法。先是有Henery和Stern兩人，指出第二名、第三名的機率與頭馬機率分別存在大約0.8和0.65的比例關係，繼而有Lo和 Bacon-Shone，公開了一條修正公式：p^c/Σp^c

公式裡的c是一個常數，計算第二名的c剛好就是0.8，計算第三名的c是0.65。

舉例，一場馬四匹馬上陣，A、B、C、D四匹馬的取勝機率為0.4、0.3、0.2、0.1，用Harville formula計算A搭B的連贏機率為：
0.4*0.3/(1-0.4)+0.3*0.4/(1-0.3)=0.3714

修正版則要先調整四匹馬的機率，
p(A)=0.4^0.8/(0.4^0.8+0.3^0.8+0.2^0.8+0.1^0.8)=0.3706
p(B)=0.3^0.8/(0.4^0.8+0.3^0.8+0.2^0.8+0.1^0.8)=0.2944

再用新的數字代入Harville formula，A搭B的連贏機率變為：
0.4*0.2944/(1-0.3706)+0.3*0.3706/(1-0.2944)=0.345

這條修正公式和《計得精彩》書裡提到的Benter Correction基本上是一樣的，不同的只是William Benter用來計算第二名的c是0.81而非0.8，計算第三名的c則同樣是0.65。修正公式的最大問題也正是在這裡，c並非一成不變的常數，用不同的data在不同的時段計算出來的c是不一樣的，這會否造成新的偏差、新的偏差有多大，又成了新的問題。

不過，話說回來，不管選用什麼版本，只要是選擇了以獨贏機率推算位置機率的做法，最重要的，還是首先要確保獨贏機率計算的準確，我們不可能幻想錯誤的獨贏機率加一個錯誤的連贏計算方法會有“負負得正”的效果，也不可能幻想一個沒有偏差的連贏計算方法建基於錯誤的獨贏機率而能取得成功。

池某知道Michael兄和Peter Pan兄平時都是主攻連贏，歡迎分享心得。
PermaLink: https://articles.zkiz.com/?id=229459

小製作　大工程

經過近四個星期日以繼夜的努力，新的賭馬model總算成形。這次更新model有兩大目的：一是希望增加model的穩定性；二是希望理順從資料採集到下注的整個流程，使整體操作更自動化、更省時、方便，且更準確。雖然還未經實戰考驗，初步看來這兩個目標還是可以達到。

所謂增加model的穩定性，就是要防止model因某方面data不足而失算時會出現過大的損失，具體解決之道還是一個“借”字，即“借”外力去彌補incomplete data所造成的偏差，但如何“補”得恰如其分而又不會喧賓奪主，則很考功夫。

前文已經說明，在expected value相若的情況下，最大損失越小的賭局，越能放心以大大注獲利。故能有效排除model出現極端損失的可能性是一個很大的進步。

從資料採集，到把data在各module間搬來搬去，再到最後結合實時賠率計算注碼下注，在操作層面看，人手輸入或手動操作的次數越少，出錯的機會就越少，要做到這一點，就要靠有效的programming來維繫。這方面，新的操作介面亦已大大改善。

其中一個改變，是把即時賠率的擷取，從馬會網頁的HTML版改為XML版。使用XML不僅run得快一些、順一些，更重要的是XML版不僅顯示賠率，還顯示具體的派彩，不像HTML版無論10.00倍還是10.95倍都一律以10倍表示就算。更detail的預計派彩，可以確保注碼分配的計算更精準。而且，使用XML版還有另外一個好處．．．，賣個關子，下次再說。


回過頭去看，其實這次改動並算不上什麼大製作，如果一路順利沒有阻滯，最多不過四、五天的工作量。這樣的小製作卻搞成了為期近一個月的大工程，實在太不應該。

小題變成大做，主要原因還是自己的知識根底不夠堅實，對不同的distribution認識不充分，對maximum likelihood等概念亦頗為模糊。缺乏清晰的認知，每每走到十字路口就躊躇不定，最後憑直覺、貪方便變成了抉擇的標準。碰巧錯誤的方法撞中一個正確的結果，問題更加嚴重，加深了積非成是的印象，更對正確的方法產生排斥，寧願一直在錯誤中打轉。

另一個原因就是programming技巧的不足。受阻於programming能力而停滯不前時，首先想到的不是攻堅克難，而是左閃右避，迂迴前進，甚至在具體做法上偷工減料，結果是令原本正確的方法扭曲變形，越錯越遠。

總結教訓：當務之急，需認真刨下書，重新掌握返STA101，同時要練習下programming，打返好個底。
PermaLink: https://articles.zkiz.com/?id=229460

懶惰心　辛苦命

十多年前池某在寺廟靜修，看過的佛門故事中，要數這個印象最深刻：

老和尚出外遠行，小和尚幫他拎行李。走了一段路，小和尚說，行李很重，想休息一會兒。老和尚說，我去找個人來幫你一把。接著，老和尚轉向一戶人家，張口就是一輪粗言穢語，然後快閃。那戶人家暴怒，抄起一根棍子追打出來，嚇得小和尚也跟著老和尚快跑，跑了很遠路程才停下來。老和尚問小和尚，行李還重嗎？小和尚說，奇怪，剛才跑的時候一點都不覺得重。



池某是典型的小和尚性格，懶得就懶，責任在身時，總是嫌三嫌四，諸多藉口，故對這個故事特別有感覺，也不時用來提醒自己，該做的事，若懶得動手，就要設法把自己推到一個不能停下來、也不能回頭的位置，這樣就能心無二念，專心一意向前行，再苦、再重的工作，都不以為苦、不以為重了。

搬來blogspot落腳之後，在過去一年多的時間，池某盡可能保持每星期至少更新一篇文章，到上周終於無以為繼，恐怕短期內亦難復舊觀，原因是，為了重整賭馬model，池某最近一直閉關埋頭苦幹，日以繼夜，做完又改，改完重做，加完又刪，刪完再加，像是沒有個了期。

重整model並非舊的不能用，而是有些新的想法，希望驗證一下。但要驗證一念的對錯，工作量是巨大的，牽一髮而動全身，由database一格一格重新執過，到逐個module改program、debug、測試，沒完沒了，而最後結果還可能是無用功，白做收場。

一想到工程艱巨，付出大而收穫沒有保證，馬上又小和尚心態作祟，總希望免得就免，推得就推，拖得就拖，潛意識裡還想偷偷向三種人學習，輕輕鬆鬆過日子：第一種，說了就當做了；第二種，幻想了就當成功了；第三種，盲信了就當無往而不利了。

但想深一層，市場上的輸家，不正是這三種人嗎？不想與這三種人為伍，唯一出路，就是拋棄懶惰心，擁抱辛苦命。把心一橫，將舊model弄死，令自己兩頭唔到岸，恢復舊model和重設新model工作量一樣大，這樣，選擇就只剩下一個，不需要心大心細了。

PermaLink: https://articles.zkiz.com/?id=229461

越窮越見鬼

計數題：一場馬有A、B、C三匹馬上陣，經過計算馬A和馬B各有50%機會取勝，馬C完全沒有機會勝出。馬A、馬B和馬C的賠率分別是2倍、2倍和5倍，應該如何下注？

驟眼一望，expected value最高的一匹馬，是0.5*2-1=0，完全找不到值得下注的機會。唔信邪？用平時最常用、最可靠的工具Kelly calculator來計一次，結果也是0%、0%、0%。顯示這是一個沒有edge的賭局。


但對於beyond兄這種賭場常客兼大戶來說，應該一眼就能看出這個賭局是個絕佳的盈利機會。不錯，只要押注10000元馬A，再押注10000元馬B，就很大機會獲得1000元的純利，5%的回報率而極低風險。這1000元的利潤來自哪裡？馬會的回扣。

日前一眾馬迷高手在池某blog裡留言討論怎樣利用回扣制度贏錢，池某覺得回扣問題也正好與前文談及的最優化資本分配公式相符，可以作為後續討論再寫一寫。

一般馬迷平時用以計算注碼的Kelly公式，亦即Kelly calculator所用的公式是：
f = (r/e-1)/(r-1)
在這裡r是real odds，e是expected odds，即win probability的倒數。

這條公式其實是最優化資本分配公式的簡化版，當涉及到回扣問題就不適用了，要回到原版找答案。

原版的最優化資本分配公式是：
f = p/a – q/b
其中，f是投入資本的最佳比例，p是盈利的機會率，即p=1/e；q是虧損的機會率，即q=1-p；a是虧損幅度；b是淨盈利率，即b=r-1。

若沒有回扣，就是a=1，這時
f=p–q/b
 =(p*b-1+p)/b
 =((r-1)/e-1+1/e))/(r-1)
 = (r/e-1)/(r-1)
就是Kelly calculator所用的公式。

若有回扣，就是a=0.9，如前文如說，一個賭局的注碼分配，很受a的變化影響。這時
f=p/0.9–q/b
 =(p*b-0.9*(1-p))/(0.9*b)
 =(p*(b+0.9)-0.9)/(0.9*b)
 =((r-0.1)/e-0.9)/(0.9*(r-1))
應投入的注碼明顯跟Kelly calculator的結果不一樣了。

以大家今天討論的“永常喜”那場為例，以池某當日得出的expected odds作基準，為了充分利用回扣，假設以100萬本金和1個Kelly來計算。

沒有回扣的注碼分配是這樣的：


有回扣的注碼分配是這樣的：


即使同樣都已把回扣計算在內，兩者的差距還是很明顯，同樣是“永常喜”勝出，有回扣版盈利要多8萬元；若是跑第二的“超越時空”勝出，有回扣版只是多輸6萬元；若是跑第三的“飛躍成功”勝出，冇回扣版要輸錢，有回扣版卻能贏錢。

故此賭馬是一個越有錢越著數，越窮越見鬼的遊戲。但賭馬也好，其他投資也好，真正的窮並非金錢上的窮，而是人窮而志窮，對固有的方法、工具和對別人的依賴形成習慣，變成心窮、智窮，以致真正的機會來到前面，也會“鬼掩眼”，反應不過來、把握不住。
PermaLink: https://articles.zkiz.com/?id=229462

狂者以不狂者為狂

中秋假期冇市，馬又星期日才跑，閒來無事，“搞史”自娛。

明代馮夢龍的《古今笑》記載了這樣一個故事：

張率年十六，作賦頌二十餘首，虞訥見而詆之。率一旦焚毀，更為詩示之，托云沈約，訥便句句嗟稱，無字不善。率曰：“此吾作也。”訥慚而退。

故事的背景是，南朝時期，有個人名叫張率，擅長詩文。有一次，他把自己寫的二十餘首詩，請一個叫虞訥的名家品評，結果被虞納彈得一文不值。張率聽了，氣上心頭，一怒之下把這些詩全燒了。夜裡張率做了一個夢，第二天心生一計，又寫了幾首詩，再送給虞訥過目，並假稱這是當時大文豪沈約的大作。虞訥一看便說句句都是佳句，字字都用得精妙。張率這才說其實是他的作品。

故事未完，這件事後來傳到沈約那裡，沈約還與張率成為朋友。沈約好奇地問張率，怎麼會想到假托他人之名這招？張率於是告訴沈約他那夜的夢境：

在夢裡張率穿越了時空去到1600年後的21世紀，這個年代人們喜歡在一種叫“博客”的媒介發表文章，張率瀏覽了一些文章之後，感受很深。他發現有些文章明明錯亂百出、狗屁不通，但只要說這就是Benjamin Graham的觀點、是巴菲特的觀點，讀者就無不稱是，無人反駁；而有些文章雖然寫得很好，像他張率的詩一樣，因作者默默無名，就被人彈得一文不值。於是張率就想到假托沈約大名之法。

沈約聽完，對張率的夢境無限嚮往。所謂心誠則靈，這夜沈約果然如願，一路美夢到天明，翌日靈感爆發，寫下了他那寥寥幾句卻意境深遠的千載不朽名篇，《狂泉》：

昔有一國，國中一水，號曰：“狂泉”。國人飲此水，無不狂；唯國君穿井而汲，獨得無恙。國人既並狂，反謂國主之不狂為狂。於是聚謀，共執國主，療其狂疾，火艾針藥，莫不畢具。國主不任其苦，於是到泉所，酌水飲之。飲畢便狂。君臣大小，其狂若一，眾乃歡然。



這次輪到張率好奇了，追問沈約的夢境。原來沈約也是夢到21世紀，在夢裡，看到有人以為學到了投資之法，像第一個發現“狂泉”的人一樣，很高興地“分享”其發現，漸漸地成為其同類的人越來越多了，但同時也有人不但不認同他們，更批評他們有問題，令他們很不安樂。他們辯稱，可以問問接觸過這種方法的人有沒有覺得不妥（相當於問飲過狂泉的人會不會承認自己是狂的），同時利用多數對少數的力量，無所不用其極，令不認同他們的人“不任其苦”，最終變成他們的同類，於是大家都心安理得了。

真是美好的大團圓結局。
PermaLink: https://articles.zkiz.com/?id=229463

追趕烏龜的蝸牛

阿基里斯是希臘神話中跑得最快的人，也就是希臘傳說中的飛人保特。不過，他的大名之所以能夠衝出希臘，為世人所熟知，卻不是因為他跑得快，反而是因為他追不上一只烏龜的故事。

故事出自公元前5世紀一位學者芝諾之手。芝諾的說法是，只要烏龜在阿基里斯前面一段距離，當阿基里斯追到烏龜原本的位置，烏龜已在同一時間段向前爬行了一段路程。如此類推，阿基里斯每次追到烏龜本來的位置，烏龜都又已向前挪動了一段距離，所以阿基里斯只能離烏龜越來越近，卻永遠也追不上烏龜。

芝諾使用的顯然是詭辯之法，但要從邏輯上駁倒芝諾悖論也不容易。芝諾主要是利用了人們對無限的抽象認知，將不能無限分割的時空作了無限分割，從而把本來輕而易舉的事說成不可能。

這種以無限來迷惑人的手法，直至2500年後的今天仍然很流行，只是做法剛好相反，不是把時空無限分割，而是把時空無限延伸，也就是當今財演大師最常用那招──無限補時，這樣就能達到相反的效果，把不可能的事說成輕而易舉。

財演大師說，買股票不必理會股價，以收股息就能達致財務自由。是否真的這麼輕而易舉呢？檢算一下就一清二楚了。

就算是追烏龜也要有個目標，以現今的購買力來算，就當1000萬港元資產是個勉強夠財務自由的目標好了。假設投資者22歲畢業，一畢業就找到工作，每個月能儲蓄5000元，之後年年加人工，每年儲蓄額增加5%；又假設他將儲蓄全數買股票收息，股票的價格永不下跌且每年能穩定收取6%的股息，並再投入股市。那麼他需要多長的時間才能達到1000萬元資產的目標呢？答案是：31年。

且慢，即使是一只烏龜爬行31年，也是一段不短的距離。既然1000萬元資產的目標，是以現今的購買力來計算，31年後的購買力當然就不一樣了。假設每年通脹率3%好了，31年之後，目標就由1000萬變了2500萬。幸好這時的資產基數已大了很多，再追11年就達到2500萬了。但11年後“烏龜”又爬到3460萬的位置，又要再追多4年。4年後“烏龜”又爬到3890萬的位置，還要再追多2年，終於追上了。

加加埋埋，要達到這個勉強夠財務自由的目標，一共要48年。也就是說，一個人22歲投身社會工作，到70歲時才能財務自由，還要假設這48年間，即使到了六、七十歲，也不會失業，還年年加人工，而且要股價永不變、週息率永不跌、通脹率永不升，才能達到。

要縮短達標時間，有兩條途徑可行：一是放棄以收股息為目標，追求更高的投資回報；二是加快工作收入的增長，像70後兄那樣，以高收入、強勁現金流“谷”大資產規模，快速達標，但這樣是以努力工作達致財務自由，並不符合大師們所說唔使do以被動現金流致財務自由的幻想。而且，以工作達致財務自由而以股息維持財務自由，也不能算是以收股息達致財務自由了。

實際上財演大師也不會、不敢行第一條路。一來，放棄以收股息為目標而轉向增長股，就是直接自打嘴巴了；二來，若股票上升導致週息率下降，他們新增的儲蓄就增值無望了，對他們來說股票真是“越升越冇價值”。故此，把口講以收股息達致財務自由的大師，最終免不了要長期逆來順受地打份牛工，或千方百計從市場之外騙些收入。

什麼以股息被動現金流達致財務自由，說得那麼牛，原來只是一只蝸牛。
PermaLink: https://articles.zkiz.com/?id=229464

淫蟲與鹹魚

公元1206年春天，蒙古乞顏部首領鐵木真統一了蒙古草原眾部族，貴族們在斡難河源頭召開大會，諸王和群臣為鐵木真上尊號“成吉思汗”，正式登基成為大蒙古國皇帝。成吉思汗封賞既畢，宰牛殺馬，大饗群臣，留下了這段記載：

飲至半酣，成吉思汗問木華黎等道：“人生世上，何事算為最樂？”木華黎道：“蕩平世界，統一乾坤，這是人生第一樂事。”成吉思汗道：“是的，但尚知其一，不知其二。”博爾朮道：“臂名鷹，控駿騎，御華服，乘著暮春天氣，出獵曠野，這也是人生樂事呢。”成吉思汗不答。博爾忽道：“鷹鸇在天空搏擊飛禽，憑騎仰觀，倒也是人生一樂。”成吉思汗仍是不答，忽必來道：“圍獵的時候，眾獸驚突，瞧著很是一樂。”成吉思汗搖頭道：“你等所說，統不及木華黎的志願，但我與木華黎有同處，亦有異處。”群臣道：“願聞主子的樂事！”成吉思汗道：“人生至樂，莫如殺滅仇敵，似摧枯木，奪他的駿馬，得他的財物，並把他妻女掠了回來，教他伴著寢室，這是最快樂的事情！”


“攪史棍”池某初次看到這段文字時相當懷疑其真實性，如果這是蒙古人所寫的歷史，竟敢毫不忌諱，直接將偉大祖先刻畫成殺人狂魔加強盜加淫蟲的形象，豈非比漢人的董狐之筆更厲害？這又是否漢人為醜化外族統治者而老作的呢？後來翻看了《蒙古秘史》所記錄的一些故事，對這段文字就不再懷疑了。

《蒙古秘史》可說是蒙古人的《舊約聖經》，從遠古傳說的蒼狼白鹿年代，即成吉思汗的22代先祖，寫至其兒子窩闊台年代，其間各個年代重重複複發生而一書再書的大事就是殺滅仇敵、奪人財物、掠人妻女，非但不必忌諱，更被寫成英雄事跡。比如成吉思汗老母訶額侖，本是他人之妻，成吉思汗老豆也速該見她貌美，就把她劫走，生下了鐵木真等四子一女。劫妻引發的仇恨也延續到下一代，以致後來鐵木真遭報復，老婆孛兒帖被仇家掠走。

為什麼仇殺、奪人財物、搶人老婆的戲碼會充斥蒙古的發展史呢？想像一下古時蒙古人的生活環境，就不難理解。他們是逐水草而居的遊牧民族，沒有固定的地盤，沒有房地產。也就是說，沒有固定資產，只有流動資產。部族的實力數人口，資產數牛羊。

搶其他部族的女人，是增強人口實力的最快方法，還可避免同一部族近親繁殖的基因缺陷；掠奪其他部族的財物，則是增加資產的最直接途徑。掠財奪妻不斷上演又加劇了部族間的仇恨，使得累積資產的風險系數高企，可以一夜破產，也可以一仗發達。鐵木真就是在被搶掠、被報復、被奪妻的高風險環境中成長、壯大，轉為報仇、搶掠、奪人妻女，佔據草原所有資產。

故此，文章開首那段對話，用今天的語言來說可以這樣理解：完成在草原的資產累積過程，達致暫時的財務自由後，成吉思汗問木華黎等，接著下來應該怎樣做？木華黎的答案是繼續累積下去，不斷擴張，有咁大贏咁大；博爾朮、博爾忽、忽必來則認為可以唔do嘆世界了。成吉思汗對博爾朮等沒有追求同條鹹魚沒分別的人生觀當場搖頭，並補充了木華黎的觀點：要擴張，同時不能忘記本來賴以成功的欲望追求和手段。

於是，有了後來的西征和滅西夏、滅金、滅宋，真正成就成吉思汗和蒙古族的偉大，且為後人所傳誦的，正是這段對話之後的歷史。如果成吉思汗也只滿足於統一草原而轉向鹹魚心態，其歷史成就最多只會跟眾多曇花一現的部族首領一樣，其資產也未必能保存得長久。

道理也就變得更顯淺了，資產，特別是流動資產，在歷史任何一個時期，對於任何一個人，都是動態的。通脹、意外、與環境的對抗、與對手的博奕，都可能造成資產的快速轉移，並不存在一個真正的“自由標準”，這一刻的財務自由，不是未來的保證。最安全的做法，是讓自己保持累積資產的追求心和戰鬥力。

那麼，那些不斷向別人灌輸財務自由就唔使do這種鹹魚心態的人，或者自己一直在打份牛工卻聲稱可以教人以投資達致財務自由的人，又或者自己以打工達致不知何種生活水平so called財務自由卻聲稱可以教投資的人，你會相信嗎？
PermaLink: https://articles.zkiz.com/?id=229465

微觀的對錯與宏觀的是非

今年馬季開鑼的日子較往年早一些，8月未完，就要根據新的變化更新程式、重整資料庫，準備迎戰新賽季了。雖然統計指標顯示，要從馬場贏錢是一年比一年困難，但對於新賽季還是不太悲觀。

不悲觀是因為對自己所處的位置很清楚。可以確定的是，自己贏不了專業的集團，也贏不了統計系的教授。所幸的是自己也並非處於食物鏈的最低端，只要遊戲的參與者之中還有拿份馬經蹲在投注站門口的老伯、或在茶餐廳“頭顎顎”望住部電視的大叔，和一大批根據電視、電台、馬經貼士下注的馬迷，贏面還是不低的。

池某當然不會當面挑戰那些老伯和大叔，一來，他們是米飯班主；二來，他們當中真的不乏藏龍臥虎之輩，有的對每一匹馬的資料熟悉得如數家珍，有的一眼就能看出哪匹馬有火、哪匹馬狀態不佳。更重要的是，他們都曾有過引以為傲的往績，一遇到質疑，即能拋出自己在哪年哪月哪日有過哪些經典之作，鎮住陣腳。

那些讓他們自豪的往績，給了他們繼續玩這個遊戲的信心、動力和熱誠，也是他們至今仍然蹲在投注站門口的原因，亦使他們一直以為自己眼光獨到、成功在望。偶然一次不大不小的收獲，更能加強他們的自信，即使這樣的收獲並不能追回之前所輸掉的損失。

他們從不會懷疑自己的眼光和方法，只會將不太如意的結果，和成功在望的目標遲遲未能實現，歸咎於運氣、騎師的發揮、馬匹走位意外等等。因此，他們也從不會反省，為什麼一年又一年，他們仍要蹲在投注站門口？

從單一的微觀的角度來看，他們也許沒有錯，甚至是其中的表表者，他們或者真的有能力找出狀態最好的馬匹，又或者通過分析計算揀中實力最強的馬匹。



不過，從整個遊戲的宏觀角度來看，狀態最好的馬匹，並不一定能就贏；實力最強的馬匹，也未必就不會輸；甚至買中了勝出的馬匹，也不一定就能贏到錢。要玩贏這個遊戲，並不在於有多高的命中率，也不在於中過幾只冷門，而是必須在大數法則之下保持優於大眾。哪年哪月哪日哪些經典之作，除了打打嘴炮贏贏牙骹，根本無助於整體身家的增長。一年又一年之後，自己的身家幾許，無法自欺欺人。

投資如打仗，玩的是排兵佈陣的遊戲，鬥的是陣法的完整、武器的精良，而不是個人在個別項目武功的高低。要贏，把握好個別指標是necessary condition，建立完整的投資系統才是sufficient condition。

在這個弱肉強食的戰場中，最怕是遇上比自己更強的陣法和更powerful的武器，最開心的是遇上自吹武功高強的義和團式莽漢，雖然以一大堆statistical models去對付手無寸鐵的老伯和大叔看似恃強凌弱、勝之不武，但既然他們自稱是武林高手，贏他們的錢倒也沒有太多的罪疚感。

醒目的讀者看到這裡應該不難察覺，把上面文章中“馬匹”二字換作“股票”，同樣是成立的，而且很可能更容易聯想到自己熟悉的老伯和大叔。
PermaLink: https://articles.zkiz.com/?id=229466

股票+股票 VS 股票+現金

前幾篇文章談到投資中兩種截然不同的情況，第一種，對於有edge的股票，盡可能分散地買，可以把Expected Growth推到最大；第二種，一注獨贏於盈利率與虧損度之比懸殊的股票，也能令資本的增長速度達至最快。究竟以一注獨贏之“矛”，對分散投資之“盾”，何者更優勝呢？那就帶著矛盾再研究吧。

一注獨贏好還是分散投資好，不僅是片面和主觀的方法之爭，把背後的條件和理據弄清楚、搞明白，對具體的操作也很有現實意義。如果可以順利解決什麼時候選擇“股票+現金”組合較有利，什麼時候選擇“股票+股票”組合較有利，也就可以間接回答Wanderer師弟所提出那條看似無從入手的難題：同2800做rebalance，用現金好，還是reits、公用股的組合好？

首先探討一下“股票+現金”組合，再次搬出最優化資本分配公式：
f = p/a – q/b
其中，f是投入資本的最佳比例，p是盈利的機會率；q是虧損的機會率；a是虧損幅度；b是淨盈利率。
相對應f這個比例，其最快增長速度，g = p*ln(1+f*b)+q*ln(1-f*a)

為了方便比較，選用上文例子中股票A的條件，假設輸贏概率都是固定的（例子中都是0.5），expected value也是固定的（例子中是0.6），這樣，就可以得出盈利率與虧損幅度之比對資金增長的影響了。

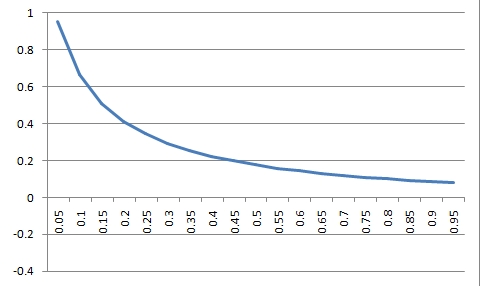
而且，因為expected value = p*b-q*a，在這個例子中p和q都為0.5，而expected value又是固定，即(b-a)是固定的，故只需考慮只其中一個變量就夠了。在一般沒經槓桿操作的賭局或股票中，虧損幅度，即a，只會處於0與1之間，所以選取a來比較會更便於解釋結果。把0<a<1代入g，就可看到“股票+現金”組合相對於虧損幅度的資金增長變化，如下圖：



現在考慮另一種選擇，“股票+股票”組合，不保留現金，把資金平均分配於兩只條件一樣但可能升跌不同步的股票A和B。同樣假設股票A和B都符合上述例子中的條件，每一輪投資不外乎四種結果：

第一種：1/4機會，A升B升，資金的收益變化是：1+0.5*b+0.5*b

第二種：1/4機會，A升B跌，資金的收益變化是：1+0.5*b-0.5*a

第三種：1/4機會，A跌B升，資金的收益變化是：1-0.5*a+0.5*b

第四種：1/4機會，A跌B跌，資金的收益變化是：1-0.5*a-0.5*a

所以，每一輪的資金增長就是：

g = 0.25*ln(1+b)+0.5*ln(1+0.5b-0.5a)+0.25*ln(1-a)

同樣把0<a<1代進去，得出“股票+股票”組合相對於虧損幅度的資金增長變化，如下圖：



想知道“矛”厲害一些，還是“盾”厲害一些，把上面兩幅圖疊起來就一清二楚了：



原來真是各有千秋，a很小，即風險很低時，一注獨贏的“股票+現金”組合（藍色線）佔盡上風；a很大，即風險很高時，也是“股票+現金”組合佔優；中度風險時，則是“股票+股票”組合（紅色線）較優。

實際操作中雖然各項參數不盡相同，但面對不同的風險程度時優化資本配置應是離不開這個大範圍的。而風險對於資本配置的影響，正正是大多數人的決策盲點。

習慣上，投資者普遍會以預期收益來主導決策，很少反過來根據風險作決策，即心存僥幸，不作最壞打算。例如收租仔加按再加按，喊一句gogogo，就以為樓價只會升不會跌；又如財演大師買完股，跳一part求雨舞（魔術師語），就幻想a=0可以不用理會。恐怕最後真是要自求多福了。
PermaLink: https://articles.zkiz.com/?id=229467

一注獨贏買乜乜

上文談及，老同學IT人以全倉一注獨贏曾取得年純利過千萬的佳績，但若攤長到十年來看，IT人的成績並不算非常突出，是什麼原因呢？是選股問題、操作問題，還是方法問題？很值得探討一番。

首先要解決的一個問題是，怎樣的股票，或說滿足什麼條件的股票，才“值得”全倉一注獨贏？又要找回那條最優化資本分配公式：
f = p/a – q/b
其中，f是投入資本的最佳比例，p是盈利的機會率；q是虧損的機會率；a是虧損幅度；b是淨盈利率。

先考慮a>=1，q>0的情況，則f = p/a-q/b < p/a < p < 1；這個結果說明了，只要有機會輸爆廠，那怕機會非常非常小，都是不能全倉一注獨贏的。

於是就可以把範圍收窄了。同時還可以看到，要f足夠大，達致全倉或非常重倉，另一個條件，是要p與q之比或b與a之比很懸殊才行。這樣的表述有點囉嗦和抽象，但能否簡單地理解為只買盈利率高的，或只買機會大、贏面高的，或結合兩者以expected value的大小來決定呢？

把上述算式通分母，得出：
f = (p*b-q*a)/(a*b)
分子的p*b-q*a，實際上就是expected value，假設為E，得出：
f = E/(a*b)

這樣就比較好理解了：第一，只有expected value為正數時，才值得投入注碼；第二，expected value越大越好，但同時不能忽略a*b的數值；第三，若expected value差不多，則a*b越小越好。

舉個例子，假設有三只股票，目前的股價都是1元：
股票A：有一半的機會升至2.6元，一半的機會跌至0.6元。
股票B：有一半的機會升至3.0元，一半的機會跌至0.2元。
股票C：有六成的機會升至3.1元，四成的機會跌至0.1元。

無論以盈利率來選擇、以機會率來選擇，還是以expected value來選擇，無疑都是股票C最凸出。實際上是否如此呢？代入公式算一算就清楚了。

股票C的expected value，E = p*b-q*a = 0.6*2.1-0.4*0.9 = 0.9
最優投資比例，f = 0.9/(2.1*0.9) = 47.62%
相對應f這個比例，其最快增長速度，g = p*ln(1+f*b)+q*ln(1-f*a)
即，g = 0.6*ln(1+0.4762*2.1)+0.4*ln(1-0.4762*0.9) = 19.2%

同樣地針對股票A和股票B算一遍，得出各自的E、f、g，見下表：



意外吧，最值得“重錘”且能令資本增長得最快的股票，並不是股票C，而是盈利率、機會率和expected value都是最低的股票A。股票B的機會率和expected value雖然都和股票A一樣，且盈利率更高，卻是最差勁的一只。

演算的結果說明了，只看某個或某些有利條件，很容易會揀錯股、買錯貨；要找出值得全倉一注獨贏的股票，更不容易；要長期成功，是難上加難。

在實際操作中，和賭波賭馬一樣，注碼的分配還有方法可依，真正令人頭疼的是expected value的估算，難中之難的是，股票每次價格變動後，a、b、p、q這些變數都是會隨之而變動的，根本無從掌握。
PermaLink: https://articles.zkiz.com/?id=229468
Next Page
ZKIZ Archives @ 2019